poniedziałek,
Arkusze Google: Tablice trygonometryczne
Generowanie tablic wartości funkcji trygonometrycznych dla określonych kątów w arkuszu kalkulacyjnym to dość proste zadanie. Jeśli wykorzystasz do tego Arkusze Google, swoje tablice zawsze będziesz mieć „przy sobie”.
W arkuszu wprowadź nagłówki oraz dwie pierwsze wartości kąta (0 i 1), jeśli chcesz wykorzystać znaki α i °, skopiuj je i wklej. Należy wprowadzić dwie pierwsze wartości, ponieważ Arkusze Google nie generują serii danych z jednego pola, a będzie to potrzebne w jednym z kolejnych kroków.

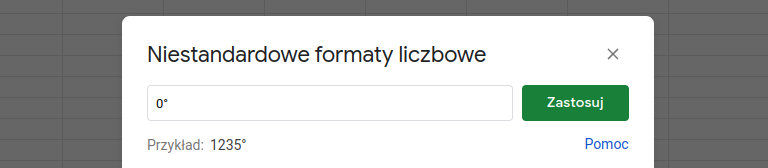
Przy wartościach miary kąta warto jednoznacznie określić jednostkę, może być ona automatycznie wstawiana przez aplikację, służy do tego mechanizm formatowania. Zaznacz obie wprowadzone wartości kątów, a następnie w menu programu wybierz kolejno „Formatuj” → „Liczba” → „Niestandardowy format liczbowy” i jako format wpisz 0°.
Ponownie zaznacz obie wprowadzone wartości kątów (0 i 1) i przeciągnij w dół kolumny mały niebieski kwadrat z prawego dolnego rogu zaznaczenia. Kolumna zostanie wypełniona serią, kolejne wartości będą automatycznie zwiększane o jeden.
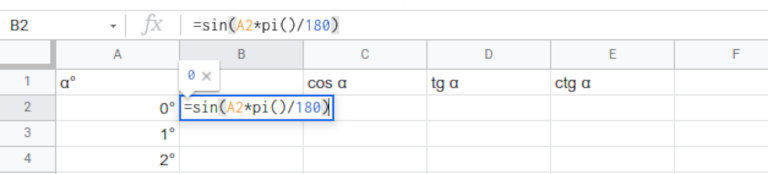
Arkusze Google mają funkcje potrzebne do wygenerowania tablic trygonometrycznych – SIN(), COS(), TAN() oraz COT(), pewnym niewielkim problemem jest to, że oczekują one argumentu wyrażonego w radianach. Istnieją dwa szybkie sposoby na zamianę radianów na stopnie, pierwszy z nich to użycie funkcji STOPNIE(), która konwertuje wartość kąta w radianach na stopnie. W prezentowanym przykładzie wykorzystano własność x [°] = x [rad] ∙ 180°/ π, wartość π zwraca funkcja PI(). Po zaznaczeniu komórki B2 wpisz do niej poniższą formułę.
=SIN(A2*pi()/180)
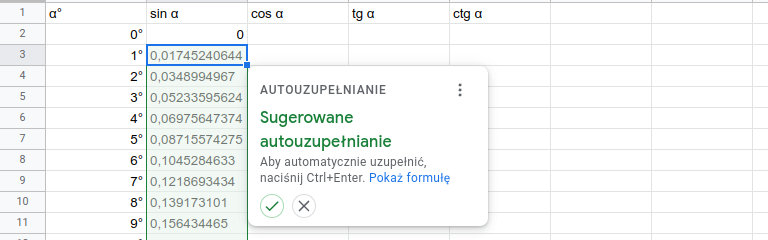
Po wpisaniu formuły i zatwierdzeniu jej klawiszem Enter, aplikacja zaproponuje automatyczne jej zastosowanie w kolejnych komórkach kolumny, wystarczy to potwierdzić. Jeśli tak się nie stanie, znasz już na to sposób polegający na przeciąganiu małego niebieskiego kwadratu w dół kolumny.
Pozostałe funkcje trygonometryczne możesz zastosować bardzo podobnie, jednak mały problem pojawi się w przypadku tangensa i cotangensa. Jak wiadomo, Pozostałe funkcje trygonometryczne możesz zastosować bardzo podobnie, jednak mały problem pojawi się w przypadku tangensa i cotangensa. Jak wiadomo, nie funkcja tangens nie jest określona dla nieparzystych wielokrotności 90°, a dla odmiany funkcja cotangens nie jest określona dla parzystych wielokrotności 90°. W przypadku generowanych tablic można to oczywiście zignorować, jednak zdecydowanie lepszym rozwiązaniem jest zastosowanie funkcji warunkowej, takiej jak np. JEŻELI(). Funkcja JEŻELI() przyjmuje trzy parametry oddzielone średnikami. Pierwszy z nich to wyrażenie logiczne, jeśli zwraca ono prawdę, przyjmowana jest wartość z drugiego argumentu, w przeciwnym wypadku zastosowany zostaje trzeci argument.
W prezentowanych poniżej formułach przyjęto, że wartości funkcji trygonometrycznych obliczane są dla kątów od 0° do 90°. Jeśli ten zakres ma być większy, należy zmodyfikować formuły, tak aby przyjrzeć się wartości sinus danego kąta w przypadku funkcji cotangens oraz jego wartości cosinus dla funkcji tangens.
=SIN(A2*pi()/180)
=COS(A2*pi()/180)
=JEŻELI(A92<>90;TAN(A92*pi()/180);"-")
=JEŻELI(A2>0;COT(A2*pi()/180);"-")
Wystarczająca wydaje się dokładność czterech miejsc po przecinku, można to ustawić za pomocą mechanizmu formatowania komórek. Aby szybko zaznaczyć wszystkie wymagające formatowania komórki, możesz użyć klawiszy strzałek w kombinacji z Ctrl oraz Shift. Zaznacz komórkę B2, wciśnij klawisze Ctrl i Shift, a następnie (przytrzymując Ctrl+Shift) naciśnij klawisz strzałki w prawo. W kolejnym kroku przytrzymaj klawisze Ctrl+Shift i naciśnij klawisz strzałki w dół. Po zaznaczeniu komórek w menu programu wybierz kolejno „Formatuj” → „Liczba” → „Niestandardowy format liczbowy” i jako format wpisz 0.0000.
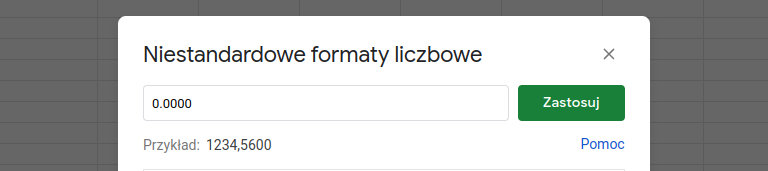
Dla wygody można dodatkowo zablokować pierwszy wiersz, znacznie podniesie to komfort pracy podczas przewijania arkusza.