sobota,
Kenneth Appel
Amerykański matematyk Kenneth Appel urodził się 8 października 1932 roku. Był pionierem w wykorzystaniu komputerów do analiz o charakterze inżynierskim. Uczył się w Queens College. W 1953 zdobył tytuł licencjata na Uniwersytecie Michigan. Karierę naukową przerwał dwuletnia służba wojskowa. W 1959 roku na macierzystej uczelni uzyskał doktorat. Pracował w Institute for Defense Analysis w Princeton, gdzie zajmował się kryptografią. Od 1961 roku był pracownikiem University of Illinois w Urbana-Champaign. Na początku lat dziewięćdziesiątych został profesorem matematyki na tej uczeni. Później podjął pracę jako szef wydziału matematycznego na University of New Hampshire w Durham. Po przejściu na emeryturę nadal udzielał się na uczelni. Zmarł 19 kwietnia 2013 roku.
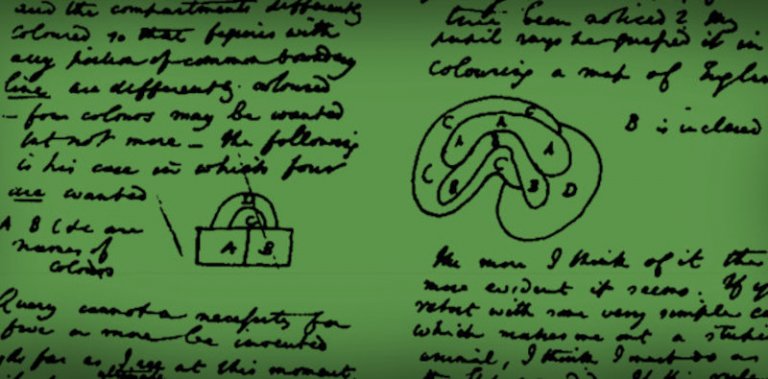
Do historii nauk ścisłych przeszedł jako współautor rozwiązania jednego z najbardziej znanych problemów matematycznych – przeprowadził pełen dowód twierdzenia o czterech barwach. Problem ten sformułował student prawa University College London Francis Guthrie w 1852 roku. Chciał on pokolorować mapę jednostek administracyjnych Anglii.
„Czy dowolną mapę polityczną na płaszczyźnie da się pokolorować czterema barwami w taki sposób, żeby każde dwa sąsiadujące regiony otrzymały różne kolory?”
–– Francis Guthrie, 1852.
Guthrie postawił hipotezę o twierdzącej odpowiedzi na powyższe pytanie, jednak nie potrafił przeprowadzić dowodu, więc zwrócił się z prośbą o pomoc do swojego profesora, którym był znany matematyk i logik Augustus De Morgan (autor powszechnie znanych praw de Morgana). De Morgan uznał „Four-Colour Problem” za bardzo interesujący, jednak nie zdołał znaleźć teoretycznego potwierdzenia hipotezy. Zwracał się z tym zagadnieniem do kolejnych matematyków. W końcu problem ten trafił na forum Londyńskiego Towarzystwa Matematycznego. W 1879 roku dowód hipotezy o czterech barwach przedstawił przyszły prezes Londyńskiego Towarzystwa Matematycznego Alfred Kempe. Po jedenastu latach odkryto błąd w dowodzie. Wtedy „Four-Colour Problem” stał się atrakcyjnym wyzwaniem dla matematyków. Mimo wielu prób nikt nie przeprowadził poprawnego dowodu przez sto lat.
W latach pięćdziesiątych ubiegłego stulecia z „Four-Colour Problem” zmierzył się niemiecki matematyk Heinrich Heesch. Doszedł do wniosku, że przeprowadzenie dowodu wymaga przeanalizowania bardzo dużej, jednak skończonej liczby przypadków. Pomysł ten stał się punktem wyjścia dla prac Kennetha Appela i Wolfganga Hakena. Wykorzystali oni superkomputer. Zastosowaną przez nich metodę można nazwać „brute force” podobnie jak znaną technikę łamania haseł. Dwaj badacze zmierzali do sprawdzenia wszystkich możliwych kombinacji. Cztery lata zajęło opracowanie potrzebnych algorytmów. W 1976 roku Appel i Haken wygenerowali oraz zweryfikowali za pomocą komputera 1936 kombinacji. Ich dowód był „brzydki” i od początku budził kontrowersje, jednak szereg niezależnych podobnych dowodów potwierdził ich osiągnięcie. Prace Appela i Hakena stały się okazją do dyskusji na temat dopuszczalnych metod dowodowych w matematyce.
Dowód „Four-Colour Problem” to spektakularne osiągnięcie matematyki komputerowej. Do dziś nikt nie udowodnił twierdzenia o czterech barwach bez komputerowego wspomagania. Jeśli w każdym „kraju” na mapie wyznaczone zostaną stolice połączone „drogami” z podobnymi ośrodkami w sąsiednich krajach, wówczas mapa polityczna ulegnie przekształceniu w graf. Takie podejście pozwala poszerzyć możliwości praktycznego stosowania twierdzenia o czterech barwach.







